Think Recursively: Solving Towers of Hanoi the Easy Way

The Towers of Hanoi is a classic mathematical puzzle that has captivated minds for centuries. In this article, we will explore the intriguing history, rules, and strategies behind this timeless puzzle. We will dive into the recursive algorithm used to solve it, understand its complexity, and explore variations that add a new twist to the challenge. Whether you are a puzzle enthusiast, a mathematics lover, or simply curious about this famous brain teaser, join us as we unravel the secrets of the Towers of Hanoi.

I. The Puzzle and Its History
II. Recursive Solution and Algorithm
III. Complexity and Variations
IV. Real-world Applications and Significance
V. Implementing the Algorithm in Different Programming Languages
Conclusion

I. The Puzzle and Its History

Puzzle Description:
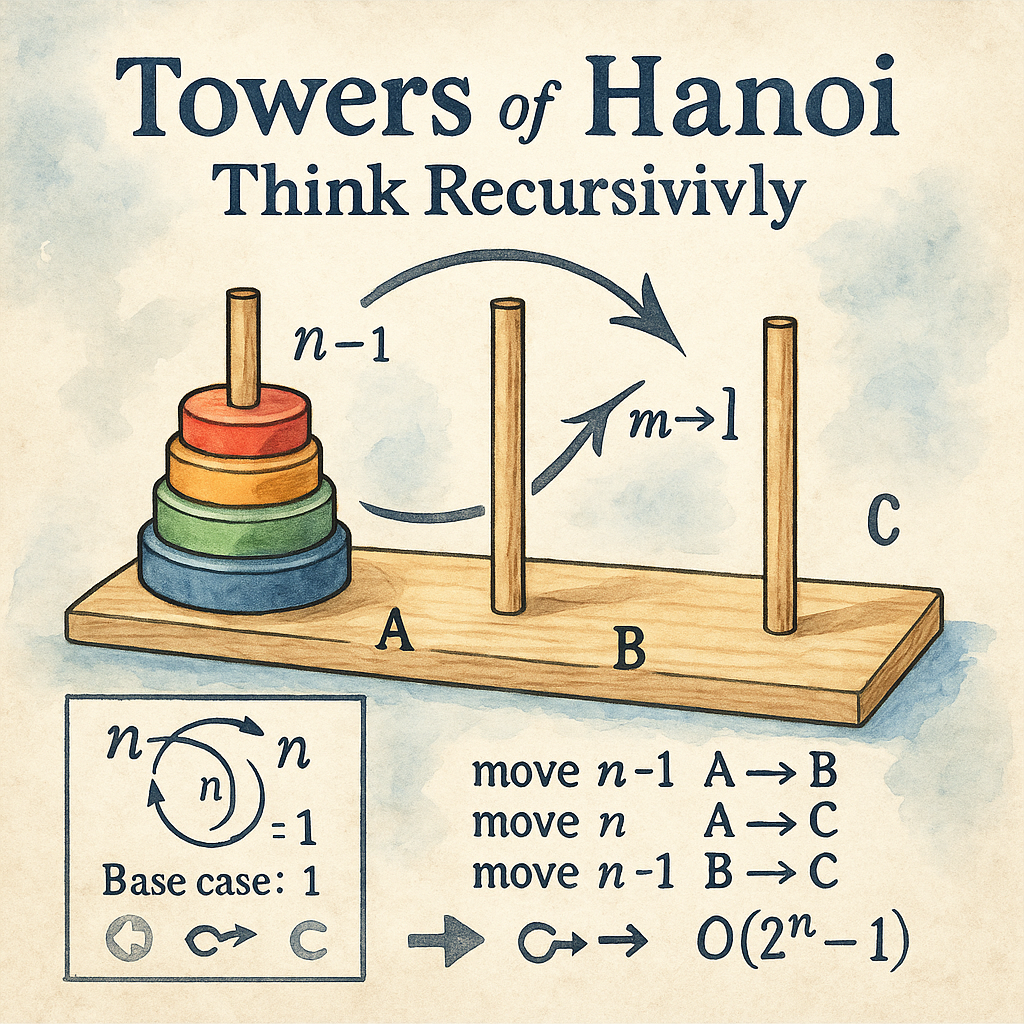
The Towers of Hanoi consists of three pegs or towers and a set of differently sized disks. The objective is to move all the disks from one tower (the source) to another (the target) with the help of a third tower (the auxiliary). The challenge lies in adhering to two rules: only one disk can be moved at a time, and a larger disk cannot be placed on top of a smaller one.

Historical Origins:
The puzzle’s origins can be traced back to ancient Indian mathematics, where it was known as the “Tower of Brahma.” In the 19th century, the French mathematician Édouard Lucas introduced the puzzle to the Western world, naming it the “Towers of Hanoi” after a Vietnamese legend about a temple with three diamond pillars and a pile of golden disks.

II. Recursive Solution and Algorithm

The Recursive Approach:
The Towers of Hanoi puzzle can be elegantly solved using a recursive algorithm. At each step, the algorithm recursively solves a smaller subproblem by moving a subset of disks to the auxiliary tower. The recursive calls continue until a base case is reached, where only a single disk is left to move. The process is then reversed to move the remaining disks to the target tower.

Algorithm Breakdown:
We explore the three steps of the recursive algorithm:

Move the top n-1 disks from the source to the auxiliary tower.
Move the largest disk from the source to the target tower.
Move the n-1 disks from the auxiliary to the target tower.

Visualization and Example:
To aid understanding, we provide a step-by-step visual example of solving the puzzle using the recursive algorithm. Diagrams or illustrations can demonstrate the movement of disks between the towers.

III. Complexity and Variations

Time Complexity:
The recursive algorithm for the Towers of Hanoi has a time complexity of O(2^n), where n is the number of disks. This exponential complexity showcases the puzzle’s inherent challenge as the number of moves grows rapidly with each additional disk.

Variations and Extensions:
We explore variations of the Towers of Hanoi puzzle, such as having more than three towers, using additional constraints, or introducing different starting configurations. These variations provide exciting new challenges and further test problem-solving skills.

IV. Real-world Applications and Significance

While the Towers of Hanoi puzzle is primarily an intellectual exercise, its principles and recursive nature have practical implications:

Algorithmic Thinking: The puzzle fosters logical and algorithmic thinking, making it a valuable tool for computer science education.
Tower of Hanoi Syndrome: The puzzle’s recursive nature has been likened to certain mental health conditions, leading to the concept of “Tower of Hanoi Syndrome” in psychology.
Tower of Hanoi in Computer Science: The puzzle serves as a benchmark problem in algorithm analysis, recursive programming, and optimization techniques.

V. Implementing the Algorithm in Different Programming Languages

Let’s demonstrate the implementation of the anagram checker algorithm in three popular programming languages: Python, JavaScript, and PHP.

PHP Solution

function towersOfHanoi($n, $source, $auxiliary, $target) {
    if ($n === 1) {
        echo "Move disk 1 from $source to $target" . PHP_EOL;
        return;
    }

    towersOfHanoi($n - 1, $source, $target, $auxiliary);

    echo "Move disk $n from $source to $target" . PHP_EOL;

    towersOfHanoi($n - 1, $auxiliary, $source, $target);
}

// Example usage:
$numDisks = 3;
$towerA = "A";
$towerB = "B";
$towerC = "C";

echo "Steps to solve the Towers of Hanoi puzzle with $numDisks disks:" . PHP_EOL;
towersOfHanoi($numDisks, $towerA, $towerB, $towerC);

JavaScript Solution

function towersOfHanoi(n, source, auxiliary, target) {
  if (n === 1) {
    console.log(`Move disk 1 from ${source} to ${target}`);
    return;
  }

  towersOfHanoi(n - 1, source, target, auxiliary);
  console.log(`Move disk ${n} from ${source} to ${target}`);
  towersOfHanoi(n - 1, auxiliary, source, target);
}

// Example usage:
const numDisks = 3;
const towerA = 'A';
const towerB = 'B';
const towerC = 'C';

console.log(`Steps to solve the Towers of Hanoi puzzle with ${numDisks} disks:`);
towersOfHanoi(numDisks, towerA, towerB, towerC);

Python Solution

def towers_of_hanoi(n, source, auxiliary, target):
    if n == 1:
        print(f"Move disk 1 from {source} to {target}")
        return

    towers_of_hanoi(n - 1, source, target, auxiliary)
    print(f"Move disk {n} from {source} to {target}")
    towers_of_hanoi(n - 1, auxiliary, source, target)

# Example usage:
num_disks = 3
tower_A = 'A'
tower_B = 'B'
tower_C = 'C'

print(f"Steps to solve the Towers of Hanoi puzzle with {num_disks} disks:")
towers_of_hanoi(num_disks, tower_A, tower_B, tower_C)

Conclusion

The Towers of Hanoi puzzle continues to captivate puzzle enthusiasts and mathematicians alike with its elegance and recursive nature. Whether you approach it as a recreational challenge or a learning opportunity, the puzzle offers insights into algorithmic thinking, recursion, and problem-solving strategies. By understanding the recursive algorithm and exploring variations, we can appreciate the puzzle’s significance and its enduring place in the realm of mathematical puzzles.

Missing Parenthesis